Abstract
Drifting Models introduce a novel generative approach where the pushforward distribution evolves during training, enabling efficient one-step inference with state-of-the-art performance on ImageNet.
Generative modeling can be formulated as learning a mapping f such that its pushforward distribution matches the data distribution. The pushforward behavior can be carried out iteratively at inference time, for example in diffusion and flow-based models. In this paper, we propose a new paradigm called Drifting Models, which evolve the pushforward distribution during training and naturally admit one-step inference. We introduce a drifting field that governs the sample movement and achieves equilibrium when the distributions match. This leads to a training objective that allows the neural network optimizer to evolve the distribution. In experiments, our one-step generator achieves state-of-the-art results on ImageNet at 256 x 256 resolution, with an FID of 1.54 in latent space and 1.61 in pixel space. We hope that our work opens up new opportunities for high-quality one-step generation.
Community
Generative Modeling via Drifting: Main Results Explained
This paper introduces Drifting Models, a new paradigm for generative modeling that shifts the iterative process from inference time to training time, enabling high-quality one-step generation.
Core Innovation: Training-Time Distribution Evolution
Unlike diffusion/flow models that perform iterative updates during inference, Drifting Models evolve the pushforward distribution during training:
Figure 1: Drifting Model Concept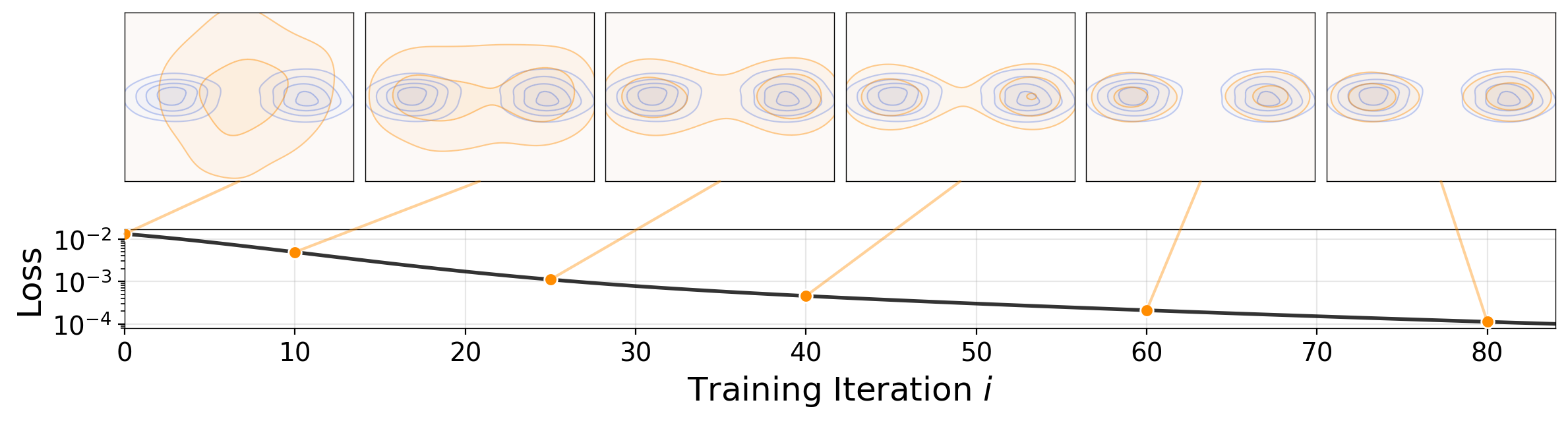
- A network
fmaps prior distributionp_priorto pushforward distributionq - Training iterates models
{f_i}→ sequences of pushforward distributions{q_i} - Drifting field approaches zero when
qmatchesp_data
Figure 2: Sample Drifting Mechanism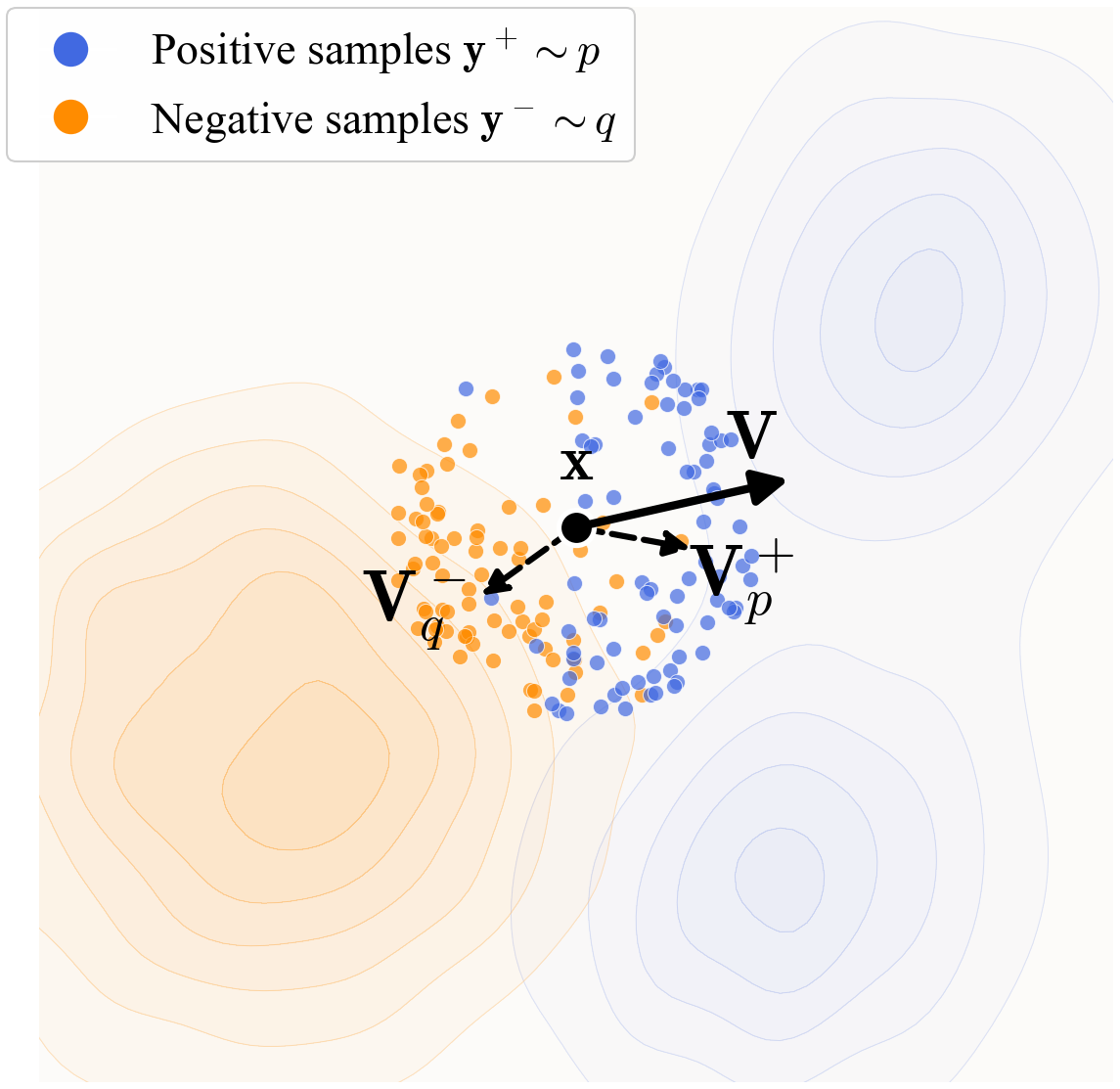
- Generated samples are attracted by data distribution (blue)
- Generated samples are repulsed by sample distribution (orange)
- Drift vector:
V = V_p+ - V_q-
Training Objective
The key insight is using an antisymmetric drifting field where:
V_{p,q}(x) = -V_{q,p}(x)- When distributions match (
p = q), drift becomes zero for all samples
Training loss minimizes drift:
L = E_ε[‖f_θ(ε) - stopgrad(f_θ(ε) + V_{p,q_θ}(f_θ(ε)))‖²]
Experimental Results
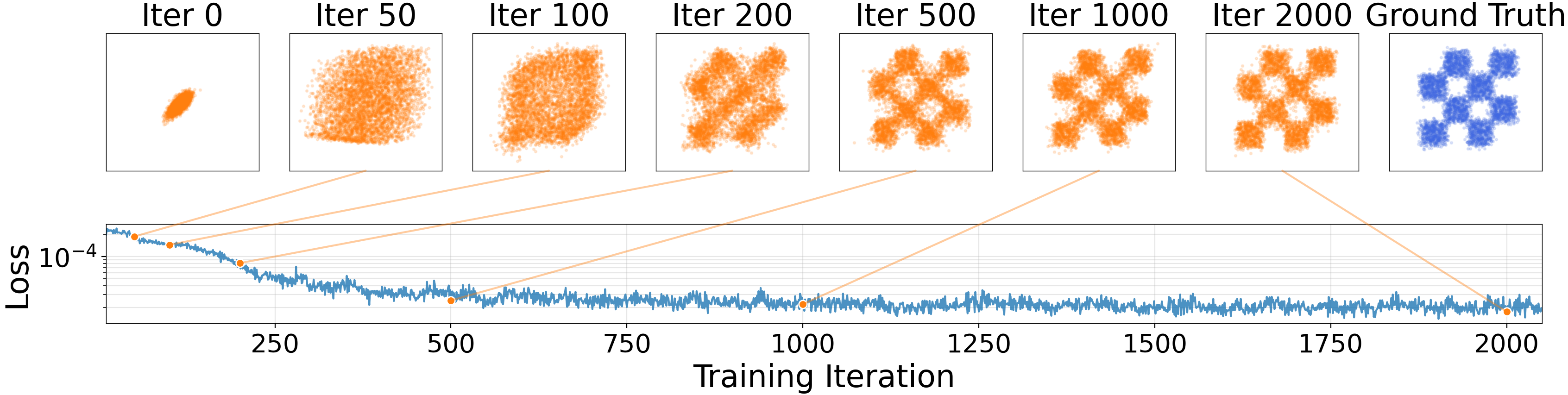
Toy Experiments Demonstrate Robustness
Figure 3: Distribution Evolution
- Shows 2D case where
qevolves toward bimodalp - No mode collapse even when initialized on single mode
- Loss (‖V‖²) decreases as distribution converges
- Demonstrates training stability
State-of-the-Art ImageNet Results
Table 5: Latent Space Generation (256×256)
| Method | Space | Params | NFE | FID ↓ | IS ↑ |
|---|---|---|---|---|---|
| Multi-step Diffusion/Flows | 250×2 | 2.27-1.13 | 262-305 | ||
| Single-step Diffusion/Flows | 1 | 34.24-1.72 | 282-284 | ||
| Drifting Models | SD-VAE | 463M | 1 | 1.54 | 258.9 |
Table 6: Pixel Space Generation (256×256)
| Method | Space | Params | NFE | FID ↓ | IS ↑ |
|---|---|---|---|---|---|
| Multi-step Diffusion/Flows | pix | 2.5B | 512×2 | 1.38-2.44 | - |
| GANs | pix | 569M | 1 | 6.95-2.30 | 152-265 |
| Drifting Models | pix | 464M | 1 | 1.61 | 307.5 |
Key Achievements
- State-of-the-art 1-NFE performance: FID 1.54 (latent) and 1.61 (pixel) outperform all previous single-step methods
- Competitive with multi-step models: Results rival even expensive multi-step diffusion models
- Robust to mode collapse: Toy experiments show stability across different initializations
- Beyond images: Successful application to robotics control tasks, matching/exceeding 100-NFE diffusion policy with 1-NFE
Technical Contributions
- Feature-space training: Uses self-supervised encoders (MAE, MoCo, SimCLR) for rich gradient signals
- Classifier-Free Guidance: Naturally supports CFG through training-time negative sampling
- Multi-scale features: Extracts drifting losses across multiple network stages
- Normalization techniques: Ensures stable training across different feature encoders
The work opens new possibilities for efficient generative modeling by reframing iterative neural network training as a distribution evolution mechanism, fundamentally different from the differential equation approach of diffusion/flow models.
Models citing this paper 0
No model linking this paper
Datasets citing this paper 0
No dataset linking this paper
Spaces citing this paper 0
No Space linking this paper
Collections including this paper 0
No Collection including this paper